API reference¶
spykeutils package¶
- class SpykeException[source]¶
Exception thrown when a function in spykeutils encounters a problem that is not covered by standard exceptions.
When using Spyke Viewer, these exceptions will be caught and shown in the GUI, while general exceptions will not be caught (and therefore be visible in the console) for easier debugging.
conversions Module¶
- analog_signal_array_to_analog_signals(signal_array)[source]¶
Return a list of analog signals for an analog signal array.
If signal_array is attached to a recording channel group with exactly is many channels as there are channels in signal_array, each created signal will be assigned the corresponding channel. If the attached recording channel group has only one recording channel, all created signals will be assigned to this channel. In all other cases, the created signal will not have a reference to a recording channel.
Note that while the created signals may have references to a segment and channels, the relationships in the other direction are not automatically created (the signals are not attached to the recording channel or segment). Other properties like annotations are not copied or referenced in the created analog signals.
Parameters: signal_array (neo.core.AnalogSignalArray) – An analog signal array from which the neo.core.AnalogSignal objects are constructed. Returns: A list of analog signals, one for every channel in signal_array. Return type: list
- epoch_array_to_epochs(epoch_array)[source]¶
Return a list of epochs for an epoch array.
Note that while the created epochs may have references to a segment, the relationships in the other direction are not automatically created (the events are not attached to the segment). Other properties like annotations are not copied or referenced in the created epochs.
Parameters: epoch_array (neo.core.EpochArray) – A period array from which the Epoch objects are constructed. Returns: A list of events, one for of the events in epoch_array. Return type: list
- event_array_to_events(event_array)[source]¶
Return a list of events for an event array.
Note that while the created events may have references to a segment, the relationships in the other direction are not automatically created (the events are not attached to the segment). Other properties like annotations are not copied or referenced in the created events.
Parameters: event_array (neo.core.EventArray) – An event array from which the Event objects are constructed. Returns: A list of events, one for of the events in event_array. Return type: list
- spike_train_to_spikes(spike_train, include_waveforms=True)[source]¶
Return a list of spikes for a spike train.
Note that while the created spikes have references to the same segment and unit as the spike train, the relationships in the other direction are not automatically created (the spikes are not attached to the unit or segment). Other properties like annotations are not copied or referenced in the created spikes.
Parameters: - spike_train (neo.core.SpikeTrain) – A spike train from which the neo.core.Spike objects are constructed.
- include_waveforms (bool) – Determines if the waveforms property is converted to the spike waveforms. If waveforms is None, this parameter has no effect.
Returns: A list of neo.core.Spike objects, one for every spike in spike_train.
Return type: list
- spikes_to_spike_train(spikes, include_waveforms=True)[source]¶
Return a spike train for a list of spikes.
All spikes must have an identical left sweep, the same unit and the same segment, otherwise a SpykeException is raised.
Note that while the created spike train has references to the same segment and unit as the spikes, the relationships in the other direction are not automatically created (the spike train is not attached to the unit or segment). Other properties like annotations are not copied or referenced in the created spike train.
Parameters: - spikes (sequence) – A sequence of neo.core.Spike objects from which the spike train is constructed.
- include_waveforms (bool) – Determines if the waveforms from the spike objects are used to fill the waveforms property of the resulting spike train. If True, all spikes need a waveform property with the same shape or a SpykeException is raised (or the waveform property needs to be None for all spikes).
Returns: All elements of spikes as spike train.
Return type:
correlations Module¶
- correlogram(trains, bin_size, max_lag=array(500.0) * ms, border_correction=True, per_second=True, unit=UnitTime('millisecond', 0.001 * s, 'ms'), progress=None)[source]¶
Return (cross-)correlograms from a dictionary of spike train lists for different units.
Parameters: - trains (dict) – Dictionary of neo.core.SpikeTrain lists.
- bin_size (Quantity scalar) – Bin size (time).
- max_lag (Quantity scalar) – Cut off (end time of calculated correlogram).
- border_correction (bool) – Apply correction for less data at higher timelags. Not perfect for bin_size != 1*``unit``, especially with large max_lag compared to length of spike trains.
- per_second (bool) – If True, counts returned are per second. Otherwise, counts per spike train are returned.
- unit (Quantity) – Unit of X-Axis.
- progress (progress_indicator.ProgressIndicator) – A ProgressIndicator object for the operation.
Returns: Two values:
- An ordered dictionary indexed with the indices of trains of ordered dictionaries indexed with the same indices. Entries of the inner dictionaries are the resulting (cross-)correlograms as numpy arrays. All crosscorrelograms can be indexed in two different ways: c[index1][index2] and c[index2][index1].
- The bins used for the correlogram calculation.
Return type: dict, Quantity 1D
progress_indicator Module¶
- exception CancelException[source]¶
Bases: exceptions.Exception
This is raised when a user cancels a progress process. It is used by ProgressIndicator and its descendants.
- class ProgressIndicator[source]¶
Bases: object
Base class for classes indicating progress of a long operation.
This class does not implement any of the methods and can be used as a dummy if no progress indication is needed.
- begin(title='')[source]¶
Signal that the operation starts.
Parameters: title (string) – The name of the whole operation.
- set_status(new_status)[source]¶
Set status description.
Parameters: new_status (string) – A description of the current status.
- ignores_cancel(function)[source]¶
Decorator for functions that should ignore a raised CancelException and just return nothing in this case
rate_estimation Module¶
- aligned_spike_trains(trains, events, copy=True)[source]¶
Return a list of spike trains aligned to an event (the event will be time 0 on the returned trains).
Parameters: - trains (list) – A list of neo.core.SpikeTrain objects.
- events (dict) – A dictionary of Event objects, indexed by segment. These events will be used to align the spike trains and will be at time 0 for the aligned spike trains.
- copy (bool) – Determines if aligned copies of the original spike trains will be returned. If not, every spike train needs exactly one corresponding event, otherwise a ValueError will be raised. Otherwise, entries with no event will be ignored.
- collapsed_spike_trains(trains)[source]¶
Return a superposition of a list of spike trains.
Parameters: trains (iterable) – A list of neo.core.SpikeTrain objects Returns: A spike train object containing all spikes of the given spike trains. Return type: neo.core.SpikeTrain
- optimal_gauss_kernel_size(train, optimize_steps, progress=None)[source]¶
Return the optimal kernel size for a spike density estimation of a spike train for a gaussian kernel. This function takes a single spike train, which can be a superposition of multiple spike trains (created with collapsed_spike_trains()) that should be included in a spike density estimation.
Implements the algorithm from (Shimazaki, Shinomoto. Journal of Computational Neuroscience. 2010).
Parameters: - train (neo.core.SpikeTrain) – The spike train for which the kernel size should be optimized.
- optimize_steps (Quantity 1D) – Array of kernel sizes to try (the best of these sizes will be returned).
- progress (progress_indicator.ProgressIndicator) – Set this parameter to report progress. Will be advanced by len(optimize_steps) steps.
Returns: Best of the given kernel sizes
Return type: Quantity scalar
- psth(trains, bin_size, rate_correction=True, start=array(0.0) * ms, stop=array(inf) * s)[source]¶
Return dictionary of peri stimulus time histograms for a dictionary of spike train lists.
Parameters: - trains (dict) – A dictionary of lists of neo.core.SpikeTrain objects.
- bin_size (Quantity scalar) – The desired bin size (as a time quantity).
- rate_correction (bool) – Determines if a rates (True) or counts (False) are returned.
- start (Quantity scalar) – The desired time for the start of the first bin. It will be recalculated if there are spike trains which start later than this time.
- stop (Quantity scalar) – The desired time for the end of the last bin. It will be recalculated if there are spike trains which end earlier than this time.
Returns: A dictionary (with the same indices as trains) of arrays containing counts (or rates if rate_correction is True) and the bin borders.
Return type: dict, Quantity 1D
- spike_density_estimation(trains, start=array(0.0) * ms, stop=None, kernel=None, kernel_size=array(100.0) * ms, optimize_steps=None, progress=None)[source]¶
Create a spike density estimation from a dictionary of lists of spike trains.
The spike density estimations give an estimate of the instantaneous rate. The density estimation is evaluated at 1024 equally spaced points covering the range of the input spike trains. Optionally finds optimal kernel size for given data using the algorithm from (Shimazaki, Shinomoto. Journal of Computational Neuroscience. 2010).
Parameters: - trains (dict) – A dictionary of neo.core.SpikeTrain lists.
- start (Quantity scalar) – The desired time for the start of the estimation. It will be recalculated if there are spike trains which start later than this time. This parameter can be negative (which could be useful when aligning on events).
- stop (Quantity scalar) – The desired time for the end of the estimation. It will be recalculated if there are spike trains which end earlier than this time.
- kernel (func or signal_processing.Kernel) – The kernel function or instance to use, should accept two parameters: A ndarray of distances and a kernel size. The total area under the kernel function should be 1. Automatic optimization assumes a Gaussian kernel and will likely not produce optimal results for different kernels. Default: Gaussian kernel
- kernel_size (Quantity scalar) – A uniform kernel size for all spike trains. Only used if optimization of kernel sizes is not used.
- optimize_steps (Quantity 1D) – An array of time lengths that will be considered in the kernel width optimization. Note that the optimization assumes a Gaussian kernel and will most likely not give the optimal kernel size if another kernel is used. If None, kernel_size will be used.
- progress (progress_indicator.ProgressIndicator) – Set this parameter to report progress.
Returns: Three values:
- A dictionary of the spike density estimations (Quantity 1D in Hz). Indexed the same as trains.
- A dictionary of kernel sizes (Quantity scalars). Indexed the same as trains.
- The used evaluation points.
Return type: dict, dict, Quantity 1D
signal_processing Module¶
- class CausalDecayingExpKernel(kernel_size=array(1.0) * s, normalize=True)[source]¶
Bases: spykeutils.signal_processing.Kernel
Unnormalized:
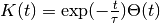 with
with
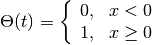 and kernel size
and kernel size 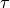 .
.Normalized to unit area:
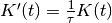
- class GaussianKernel(kernel_size=array(1.0) * s, normalize=True)[source]¶
Bases: spykeutils.signal_processing.SymmetricKernel
Unnormalized:
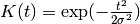 with kernel
size
with kernel
size 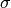 (corresponds to the standard deviation of a Gaussian
distribution).
(corresponds to the standard deviation of a Gaussian
distribution).Normalized to unit area:
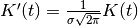
- class Kernel(kernel_size, normalize)[source]¶
Bases: object
Base class for kernels.
- boundary_enclosing_at_least(fraction)[source]¶
Calculates the boundary
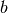 so that the integral from
so that the integral from
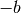 to
to 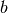 encloses at least a certain fraction of the
integral over the complete kernel.
encloses at least a certain fraction of the
integral over the complete kernel.Parameters: fraction (float) – Fraction of the whole area which at least has to be enclosed. Returns: boundary Return type: Quantity scalar
- normalization_factor(kernel_size)[source]¶
Returns the factor needed to normalize the kernel to unit area.
Parameters: kernel_size (Quantity scalar) – Controls the width of the kernel. Returns: Factor to normalize the kernel to unit width. Return type: Quantity scalar
- summed_dist_matrix(vectors, presorted=False)[source]¶
Calculates the sum of all element pair distances for each pair of vectors.
If
 and
and 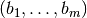 are the
are the
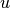 -th and
-th and  -th vector from vectors and
-th vector from vectors and 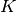 the
kernel, the resulting entry in the 2D array will be
the
kernel, the resulting entry in the 2D array will be 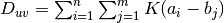 .
.Parameters: - vectors (sequence) – A sequence of Quantity 1D to calculate the summed distances for each pair. The required units depend on the kernel. Usually it will be the inverse unit of the kernel size.
- presorted (bool) – Some optimized specializations of this function may need sorted vectors. Set presorted to True if you know that the passed vectors are already sorted to skip the sorting and thus increase performance.
Return type: Quantity 2D
- class KernelFromFunction(kernel_func, kernel_size)[source]¶
Bases: spykeutils.signal_processing.Kernel
Creates a kernel form a function. Please note, that not all methods for such a kernel are implemented.
- class LaplacianKernel(kernel_size=array(1.0) * s, normalize=True)[source]¶
Bases: spykeutils.signal_processing.SymmetricKernel
Unnormalized:
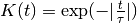 with kernel size
with kernel size
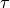 .
.Normalized to unit area:
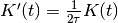
- class RectangularKernel(half_width=array(1.0) * s, normalize=True)[source]¶
Bases: spykeutils.signal_processing.SymmetricKernel
Unnormalized:
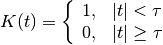 with kernel size
with kernel size 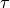 corresponding to the half width.
corresponding to the half width.Normalized to unit area:
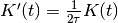
- class SymmetricKernel(kernel_size, normalize)[source]¶
Bases: spykeutils.signal_processing.Kernel
Base class for symmetric kernels.
- class TriangularKernel(half_width=array(1.0) * s, normalize=True)[source]¶
Bases: spykeutils.signal_processing.SymmetricKernel
Unnormalized:
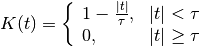 with kernel size
with kernel size 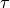 corresponding to the half width.
corresponding to the half width.Normalized to unit area:
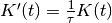
- as_kernel_of_size(obj, kernel_size)[source]¶
Returns a kernel of desired size.
Parameters: - obj (Kernel or func) – Either an existing kernel or a kernel function. A kernel function takes two arguments. First a Quantity 1D of evaluation time points and second a kernel size.
- kernel_size (Quantity 1D) – Desired size of the kernel.
Returns: A Kernel with the desired kernel size. If obj is already a Kernel instance, a shallow copy of this instance with changed kernel size will be returned. If obj is a function it will be wrapped in a Kernel instance.
Return type:
- discretize_kernel(kernel, sampling_rate, area_fraction=0.99999, num_bins=None, ensure_unit_area=False)[source]¶
Discretizes a kernel.
Parameters: - kernel (Kernel or function) – The kernel or kernel function. If a kernel function is used it should take exactly one 1-D array as argument.
- area_fraction (float) – Fraction between 0 and 1 (exclusive) of the integral of the kernel which will be at least covered by the discretization. Will be ignored if num_bins is not None. If area_fraction is used, the kernel has to provide a method boundary_enclosing_at_least() (see Kernel.boundary_enclosing_at_least()).
- sampling_rate (Quantity scalar) – Sampling rate for the discretization. The unit will typically be a frequency unit.
- num_bins (int) – Number of bins to use for the discretization.
- ensure_unit_area (bool) – If True, the area of the discretized kernel will be normalized to 1.0.
Return type: Quantity 1D
- smooth(binned, kernel, sampling_rate, mode='same', **kernel_discretization_params)[source]¶
Smoothes a binned representation (e.g. of a spike train) by convolving with a kernel.
Parameters: - binned (1-D array) – Bin array to smooth.
- kernel (Kernel) – The kernel instance to convolve with.
- sampling_rate (Quantity scalar) – The sampling rate which will be used to discretize the kernel. It should be equal to the sampling rate used to obtain binned. The unit will typically be a frequency unit.
- mode ({‘same’, ‘full’, ‘valid’}) –
- ‘same’: The default which returns an array of the same size as binned
- ‘full’: Returns an array with a bin for each shift where binned and the discretized kernel overlap by at least one bin.
- ‘valid’: Returns only the discretization bins where the discretized kernel and binned completely overlap.
See also numpy.convolve.
- kernel_discretization_params (dict) – Additional discretization arguments which will be passed to discretize_kernel().
Returns: The smoothed representation of binned.
Return type: Quantity 1D
- st_convolve(train, kernel, sampling_rate, mode='same', binning_params={}, kernel_discretization_params={})[source]¶
Convolves a neo.core.SpikeTrain with a kernel.
Parameters: - train (neo.core.SpikeTrain) – Spike train to convolve.
- kernel (Kernel) – The kernel instance to convolve with.
- sampling_rate (Quantity scalar) – The sampling rate which will be used to bin the spike train. The unit will typically be a frequency unit.
- mode ({‘same’, ‘full’, ‘valid’}) –
- ‘same’: The default which returns an array covering the whole duration of the spike train train.
- ‘full’: Returns an array with additional discretization bins in the beginning and end so that for each spike the whole discretized kernel is included.
- ‘valid’: Returns only the discretization bins where the discretized kernel and spike train completely overlap.
See also scipy.signal.convolve().
- binning_params (dict) – Additional discretization arguments which will be passed to tools.bin_spike_trains().
- kernel_discretization_params (dict) – Additional discretization arguments which will be passed to discretize_kernel().
Returns: The convolved spike train, the boundaries of the discretization bins
Return type: (Quantity 1D, Quantity 1D with the inverse units of sampling_rate)
spike_train_generation Module¶
- gen_homogeneous_poisson(rate, t_start=array(0.0) * s, t_stop=None, max_spikes=None, refractory=array(0.0) * s)[source]¶
Generate a homogeneous Poisson spike train. The length is controlled with t_stop and max_spikes. Either one or both of these arguments have to be given.
Parameters: - rate (Quantity scalar) – Average firing rate of the spike train to generate as frequency scalar.
- t_start (Quantity scalar) – Time at which the spike train begins as time scalar. The first actual spike will be greater than this time.
- t_stop (Quantity scalar) – Time at which the spike train ends as time scalar. All generated spikes will be lower or equal than this time. If set to None, the number of generated spikes is controlled by max_spikes and t_stop will be equal to the last generated spike.
- max_spikes – Maximum number of spikes to generate. Fewer spikes might be generated in case t_stop is also set.
- refractory (Quantity scalar) – Absolute refractory period as time scalar. No spike will follow another spike for the given duration. Afterwards the firing rate will instantaneously be set to rate again.
Returns: The generated spike train.
Return type:
- gen_inhomogeneous_poisson(modulation, max_rate, t_start=array(0.0) * s, t_stop=None, max_spikes=None, refractory=array(0.0) * s)[source]¶
Generate an inhomogeneous Poisson spike train. The length is controlled with t_stop and max_spikes. Either one or both of these arguments have to be given.
Parameters: - modulation (function) – Function
![f((t_1, \dots, t_n)):
[\text{t\_start}, \text{t\_end}]^n \rightarrow [0, 1]^n](../_images/math/41b37d78ccb1b736e68569c762fac59f9086cb94.png) giving
the instantaneous firing rates at times
giving
the instantaneous firing rates at times  as
proportion of max_rate. Thus, a 1-D array will be passed to the
function and it should return an array of the same size.
as
proportion of max_rate. Thus, a 1-D array will be passed to the
function and it should return an array of the same size. - max_rate (Quantity scalar) – Maximum firing rate of the spike train to generate as frequency scalar.
- t_start (Quantity scalar) – Time at which the spike train begins as time scalar. The first actual spike will be greater than this time.
- t_stop (Quantity scalar) – Time at which the spike train ends as time scalar. All generated spikes will be lower or equal than this time. If set to None, the number of generated spikes is controlled by max_spikes and t_stop will be equal to the last generated spike.
- refractory (Quantity scalar) – Absolute refractory period as time scalar. No spike will follow another spike for the given duration. Afterwards the firing rate will instantaneously be set to rate again.
Returns: The generated spike train.
Return type: - modulation (function) – Function
spike_train_metrics Module¶
- cs_dist(trains, smoothing_filter, sampling_rate, filter_area_fraction=0.99999)[source]¶
Calculates the Cauchy-Schwarz distance between two spike trains given a smoothing filter.
Let
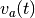 and
and 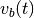 with
with 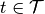 be
the spike trains convolved with some smoothing filter and
be
the spike trains convolved with some smoothing filter and 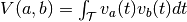 . Then, the Cauchy-Schwarz distance
of the spike trains is defined as
. Then, the Cauchy-Schwarz distance
of the spike trains is defined as 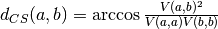 .
.The Cauchy-Schwarz distance is closely related to the Schreiber et al. similarity measure
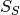 by
by 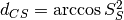
This function numerically convolves the spike trains with the smoothing filter which can be quite slow and inaccurate. If the analytical result of the autocorrelation of the smoothing filter is known, one can use schreiber_similarity() for a more efficient and precise calculation.
Further information can be found in Paiva, A. R. C., Park, I., & Principe, J. (2010). Inner products for representation and learning in the spike train domain. Statistical Signal Processing for Neuroscience and Neurotechnology, Academic Press, New York.
Parameters: - trains (sequence) – Sequence of neo.core.SpikeTrain objects of which the distance will be calculated pairwise.
- smoothing_filter (signal_processing.Kernel) – Smoothing filter to be convolved with the spike trains.
- sampling_rate (Quantity scalar) – The sampling rate which will be used to bin the spike trains as inverse time scalar.
- filter_area_fraction (float) – A value between 0 and 1 which controls the interval over which the smoothing filter will be discretized. At least the given fraction of the complete smoothing filter area will be covered. Higher values can lead to more accurate results (besides the sampling rate).
Returns: Matrix containing the Cauchy-Schwarz distance of all pairs of spike trains
Return type: 2-D array
- event_synchronization(trains, tau=None, kernel=signal_processing.RectangularKernel(1.0, normalize=False), sort=True)[source]¶
Calculates the event synchronization.
Let
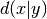 be the count of spikes in
be the count of spikes in 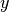 which occur shortly
before an event in
which occur shortly
before an event in 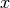 with a time difference of less than
with a time difference of less than
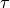 . Moreover, let
. Moreover, let 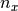 and
and 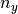 be the number of
total spikes in the spike trains
be the number of
total spikes in the spike trains 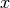 and
and 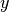 . The event
synchrony is then defined as
. The event
synchrony is then defined as 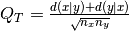 .
.The time maximum time lag
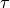 can be determined automatically for
each pair of spikes
can be determined automatically for
each pair of spikes 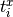 and
and 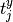 by the formula
by the formula

Further and more detailed information can be found in Quiroga, R. Q., Kreuz, T., & Grassberger, P. (2002). Event synchronization: a simple and fast method to measure synchronicity and time delay patterns. Physical Review E, 66(4), 041904.
Parameters: - trains (sequence) – Sequence of neo.core.SpikeTrain objects of which the van Rossum distance will be calculated pairwise.
- tau (Quantity scalar) – The maximum time lag for two spikes to be considered coincident or synchronous as time scalar. To have it determined automatically by above formula set it to None.
- kernel (signal_processing.Kernel) – Kernel to use in the calculation of the distance.
- sort (bool) – Spike trains with sorted spike times are be needed for the calculation. You can set sort to False if you know that your spike trains are already sorted to decrease calculation time.
Returns: Matrix containing the event synchronization for all pairs of spike trains.
Return type: 2-D array
- hunter_milton_similarity(trains, tau=array(1.0) * s, kernel=None)[source]¶
Calculates the Hunter-Milton similarity measure.
If the kernel function is denoted as
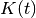 , a function
, a function 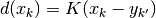 can be defined with
can be defined with 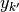 being the closest
spike in spike train
being the closest
spike in spike train 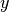 to the spike
to the spike 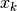 in spike train
in spike train
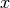 . With this the Hunter-Milton similarity measure is
. With this the Hunter-Milton similarity measure is 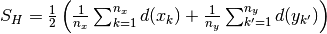 .
.This implementation returns 0 if one of the spike trains is empty, but 1 if both are empty.
Further information can be found in
- Hunter, J. D., & Milton, J. G. (2003). Amplitude and Frequency Dependence of Spike Timing: Implications for Dynamic Regulation. Journal of Neurophysiology.
- Dauwels, J., Vialatte, F., Weber, T., & Cichocki, A. (2009). On similarity measures for spike trains. Advances in Neuro-Information Processing, 177-185.
Parameters: - trains (sequence) – Sequence of neo.core.SpikeTrain objects of which the Hunter-Milton similarity will be calculated pairwise.
- tau (Quantity scalar) – The time scale for determining the coincidence of two events as time scalar.
- kernel (signal_processing.Kernel) – Kernel to use in the calculation of the distance. If None, a unnormalized Laplacian kernel will be used.
Returns: Matrix containing the Hunter-Milton similarity for all pairs of spike trains.
Return type: 2-D array
- norm_dist(trains, smoothing_filter, sampling_rate, filter_area_fraction=0.99999)[source]¶
Calculates the norm distance between spike trains given a smoothing filter.
Let
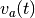 and
and 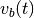 with
with 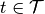 be
the spike trains convolved with some smoothing filter. Then, the norm
distance of the spike trains is defined as
be
the spike trains convolved with some smoothing filter. Then, the norm
distance of the spike trains is defined as 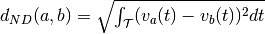 .
.Further information can be found in Paiva, A. R. C., Park, I., & Principe, J. (2010). Inner products for representation and learning in the spike train domain. Statistical Signal Processing for Neuroscience and Neurotechnology, Academic Press, New York.
Parameters: - trains (sequence) – Sequence of neo.core.SpikeTrain objects of which the distance will be calculated pairwise.
- smoothing_filter (signal_processing.Kernel) – Smoothing filter to be convolved with the spike trains.
- sampling_rate (Quantity scalar) – The sampling rate which will be used to bin the spike trains as inverse time scalar.
- filter_area_fraction (float) – A value between 0 and 1 which controls the interval over which the smoothing filter will be discretized. At least the given fraction of the complete smoothing filter area will be covered. Higher values can lead to more accurate results (besides the sampling rate).
Returns: Matrix containing the norm distance of all pairs of spike trains given the smoothing_filter.
Return type: Quantity 2D with units depending on the smoothing filter (usually temporal frequency units)
- schreiber_similarity(trains, kernel, sort=True)[source]¶
Calculates the Schreiber et al. similarity measure between spike trains given a kernel.
Let
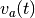 and
and 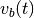 with
with 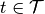 be
the spike trains convolved with some smoothing filter and
be
the spike trains convolved with some smoothing filter and 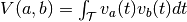 . The autocorrelation of the
smoothing filter corresponds to the kernel used to analytically calculate
the Schreiber et al. similarity measure. It is defined as
. The autocorrelation of the
smoothing filter corresponds to the kernel used to analytically calculate
the Schreiber et al. similarity measure. It is defined as 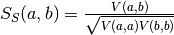 . It is closely related to
the Cauchy-Schwarz distance
. It is closely related to
the Cauchy-Schwarz distance 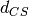 by
by 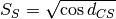 .
.In opposite to cs_dist() which numerically convolves the spike trains with a smoothing filter, this function directly uses the kernel resulting from the smoothing filter’s autocorrelation. This allows a more accurate and faster calculation.
Further information can be found in:
- Dauwels, J., Vialatte, F., Weber, T., & Cichocki, A. (2009). On similarity measures for spike trains. Advances in Neuro-Information Processing, 177-185.
- Paiva, A. R. C., Park, I., & Principe, J. C. (2009). A comparison of binless spike train measures. Neural Computing and Applications, 19(3), 405-419. doi:10.1007/s00521-009-0307-6
Parameters: - trains (sequence) – Sequence of neo.core.SpikeTrain objects of which the distance will be calculated pairwise.
- kernel (signal_processing.Kernel) – Kernel to use. It corresponds to a smoothing filter by being the autocorrelation of such a filter.
- sort (bool) – Spike trains with sorted spike times will be needed for the calculation. You can set sort to False if you know that your spike trains are already sorted to decrease calculation time.
Returns: Matrix containing the Schreiber et al. similarity measure of all pairs of spike trains.
Return type: 2-D array
- st_inner(a, b, smoothing_filter, sampling_rate, filter_area_fraction=0.99999)[source]¶
Calculates the inner product of spike trains given a smoothing filter.
Let
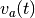 and
and 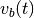 with
with 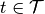 be
the spike trains convolved with some smoothing filter. Then, the inner
product of the spike trains is defined as
be
the spike trains convolved with some smoothing filter. Then, the inner
product of the spike trains is defined as 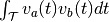 .
.Further information can be found in Paiva, A. R. C., Park, I., & Principe, J. (2010). Inner products for representation and learning in the spike train domain. Statistical Signal Processing for Neuroscience and Neurotechnology, Academic Press, New York.
Parameters: - a (sequence) – Sequence of neo.core.SpikeTrain objects.
- b (sequence) – Sequence of neo.core.SpikeTrain objects.
- smoothing_filter (signal_processing.Kernel) – A smoothing filter to be convolved with the spike trains.
- sampling_rate (Quantity scalar) – The sampling rate which will be used to bin the spike train as inverse time scalar.
- filter_area_fraction (float) – A value between 0 and 1 which controls the interval over which the smoothing_filter will be discretized. At least the given fraction of the complete smoothing_filter area will be covered. Higher values can lead to more accurate results (besides the sampling rate).
Returns: Matrix containing the inner product for each pair of spike trains with one spike train from a and the other one from b.
Return type: Quantity 2D with units depending on the smoothing filter (usually temporal frequency units)
- st_norm(train, smoothing_filter, sampling_rate, filter_area_fraction=0.99999)[source]¶
Calculates the spike train norm given a smoothing filter.
Let
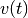 with
with 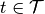 be a spike train
convolved with some smoothing filter. Then, the norm of the spike train is
defined as
be a spike train
convolved with some smoothing filter. Then, the norm of the spike train is
defined as 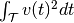 .
.Further information can be found in Paiva, A. R. C., Park, I., & Principe, J. (2010). Inner products for representation and learning in the spike train domain. Statistical Signal Processing for Neuroscience and Neurotechnology, Academic Press, New York.
Parameters: - train (neo.core.SpikeTrain) – Spike train of which to calculate the norm.
- smoothing_filter (signal_processing.Kernel) – Smoothing filter to be convolved with the spike train.
- sampling_rate (Quantity scalar) – The sampling rate which will be used to bin the spike train as inverse time scalar.
- filter_area_fraction (float) – A value between 0 and 1 which controls the interval over which the smoothing filter will be discretized. At least the given fraction of the complete smoothing filter area will be covered. Higher values can lead to more accurate results (besides the sampling rate).
Returns: The norm of the spike train given the smoothing_filter.
Return type: Quantity scalar with units depending on the smoothing filter (usually temporal frequency units)
- van_rossum_dist(trains, tau=array(1.0) * s, kernel=None, sort=True)[source]¶
Calculates the van Rossum distance.
It is defined as Euclidean distance of the spike trains convolved with a causal decaying exponential smoothing filter. A detailed description can be found in Rossum, M. C. W. (2001). A novel spike distance. Neural Computation, 13(4), 751-763. This implementation is normalized to yield a distance of 1.0 for the distance between an empty spike train and a spike train with a single spike. Divide the result by sqrt(2.0) to get the normalization used in the cited paper.
Given
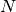 spike trains with
spike trains with 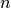 spikes on average the run-time
complexity of this function is
spikes on average the run-time
complexity of this function is 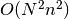 . An implementation in
. An implementation in
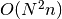 would be possible but has a high constant factor rendering
it slower in practical cases.
would be possible but has a high constant factor rendering
it slower in practical cases.Parameters: - trains (sequence) – Sequence of neo.core.SpikeTrain objects of which the van Rossum distance will be calculated pairwise.
- tau (Quantity scalar) – Decay rate of the exponential function as time scalar. Controls for which time scale the metric will be sensitive. This parameter will be ignored if kernel is not None. May also be scipy.inf which will lead to only measuring differences in spike count.
- kernel (signal_processing.Kernel) – Kernel to use in the calculation of the distance. This is not the smoothing filter, but its autocorrelation. If kernel is None, an unnormalized Laplacian kernel with a size of tau will be used.
- sort (bool) – Spike trains with sorted spike times might be needed for the calculation. You can set sort to False if you know that your spike trains are already sorted to decrease calculation time.
Returns: Matrix containing the van Rossum distances for all pairs of spike trains.
Return type: 2-D array
- van_rossum_multiunit_dist(units, weighting, tau=array(1.0) * s, kernel=None)[source]¶
Calculates the van Rossum multi-unit distance.
The single-unit distance is defined as Euclidean distance of the spike trains convolved with a causal decaying exponential smoothing filter. A detailed description can be found in Rossum, M. C. W. (2001). A novel spike distance. Neural Computation, 13(4), 751-763. This implementation is normalized to yield a distance of 1.0 for the distance between an empty spike train and a spike train with a single spike. Divide the result by sqrt(2.0) to get the normalization used in the cited paper.
Given the
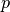 - and
- and 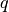 -th spike train of a and respectively
b let
-th spike train of a and respectively
b let 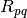 be the squared single-unit distance between these
two spike trains. Then the multi-unit distance is
be the squared single-unit distance between these
two spike trains. Then the multi-unit distance is 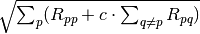 with
with  being
equal to weighting. The weighting parameter controls the interpolation
between a labeled line and a summed population coding.
being
equal to weighting. The weighting parameter controls the interpolation
between a labeled line and a summed population coding.More information can be found in Houghton, C., & Kreuz, T. (2012). On the efficient calculation of van Rossum distances. Network: Computation in Neural Systems, 23(1-2), 48-58.
Given
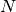 spike trains in total with
spike trains in total with 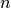 spikes on average the
run-time complexity of this function is
spikes on average the
run-time complexity of this function is 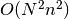 and
and 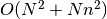 memory will be needed.
memory will be needed.Parameters: - units (dict) – Dictionary of sequences with each sequence containing the trials of one unit. Each trial should be a neo.core.SpikeTrain and all units should have the same number of trials.
- weighting (float) – Controls the interpolation between a labeled line and a summed population coding.
- tau (Quantity scalar) – Decay rate of the exponential function as time scalar. Controls for which time scale the metric will be sensitive. This parameter will be ignored if kernel is not None. May also be scipy.inf which will lead to only measuring differences in spike count.
- kernel (signal_processing.Kernel) – Kernel to use in the calculation of the distance. This is not the smoothing filter, but its autocorrelation. If kernel is None, an unnormalized Laplacian kernel with a size of tau will be used.
Returns: A 2D array with the multi-unit distance for each pair of trials.
Return type: 2D arrary
- victor_purpura_dist(trains, q=array(1.0) * Hz, kernel=None, sort=True)[source]¶
Calculates the Victor-Purpura’s (VP) distance. It is often denoted as
![D^{\text{spike}}[q]](../_images/math/dfac2903ad446eb48b50ffc294a256247bacc895.png) .
.It is defined as the minimal cost of transforming spike train a into spike train b by using the following operations:
- Inserting or deleting a spike (cost 1.0).
- Shifting a spike from
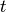 to
to 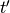 (cost
(cost 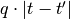 ).
).
A detailed description can be found in Victor, J. D., & Purpura, K. P. (1996). Nature and precision of temporal coding in visual cortex: a metric-space analysis. Journal of Neurophysiology.
Given the average number of spikes
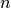 in a spike train and
in a spike train and 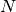 spike trains the run-time complexity of this function is
spike trains the run-time complexity of this function is
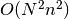 and
and 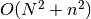 memory will be needed.
memory will be needed.Parameters: - trains (sequence) – Sequence of neo.core.SpikeTrain objects of which the distance will be calculated pairwise.
- q (Quantity scalar) – Cost factor for spike shifts as inverse time scalar. If kernel is not None, q will be ignored.
- kernel (signal_processing.Kernel) – Kernel to use in the calculation of the distance. If kernel is None, an unnormalized triangular kernel with a half width of 2.0/q will be used.
- sort (bool) – Spike trains with sorted spike times will be needed for the calculation. You can set sort to False if you know that your spike trains are already sorted to decrease calculation time.
Returns: Matrix containing the VP distance of all pairs of spike trains.
Return type: 2-D array
- victor_purpura_multiunit_dist(units, reassignment_cost, q=array(1.0) * Hz, kernel=None)[source]¶
Calculates the Victor-Purpura’s (VP) multi-unit distance.
It is defined as the minimal cost of transforming the spike trains a into spike trains b by using the following operations:
- Inserting or deleting a spike (cost 1.0).
- Shifting a spike from
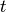 to
to 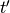 (cost
(cost 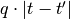 ).
). - Moving a spike to another spike train (cost reassignment_cost).
A detailed description can be found in Aronov, D. (2003). Fast algorithm for the metric-space analysis of simultaneous responses of multiple single neurons. Journal of Neuroscience Methods.
Given the average number of spikes
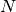 in a spike train and
in a spike train and 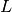 units with
units with 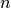 spike trains each the run-time complexity is
spike trains each the run-time complexity is
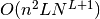 . The space complexity is
. The space complexity is 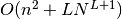 .
.For calculating the distance between only two units one should use victor_purpura_dist() which is more efficient.
Parameters: - units (dict) – Dictionary of sequences with each sequence containing the trials of one unit. Each trial should be a neo.core.SpikeTrain and all units should have the same number of trials.
- reassignment_cost (float) – Cost to reassign a spike from one train to
another (sometimes denoted with
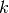 ). Should be between 0 and 2.
For 0 spikes can be reassigned without any cost, for 2 and above it is
cheaper to delete and reinsert a spike.
). Should be between 0 and 2.
For 0 spikes can be reassigned without any cost, for 2 and above it is
cheaper to delete and reinsert a spike. - q (Quantity scalar) – Cost factor for spike shifts as inverse time scalar. If kernel is not None, q will be ignored.
- kernel (signal_processing.Kernel) – Kernel to use in the calculation of the distance. If kernel is None, an unnormalized triangular kernel with a half width of 2.0/q will be used.
Returns: A 2D array with the multi-unit distance for each pair of trials.
Return type: 2D arrary
sorting_quality_assesment Module¶
Functions for estimating the quality of spike sorting results. These functions estimate false positive and false negative fractions.
- calculate_refperiod_fp(num_spikes, refperiod, violations, total_time)[source]¶
Return the rate of false positives calculated from refractory period calculations for each unit. The equation used is described in (Hill et al. The Journal of Neuroscience. 2011).
Parameters: - num_spikes (dict) – Dictionary of total number of spikes, indexed by unit.
- refperiod (Quantity scalar) – The refractory period (time). If the spike sorting algorithm includes a censored period (a time after a spike during which no new spikes can be found), subtract it from the refractory period before passing it to this function.
- violations (dict) – Dictionary of total number of violations, indexed the same as num_spikes.
- total_time (Quantity scalar) – The total time in which violations could have occured.
Returns: A dictionary of false positive rates indexed by unit. Note that values above 0.5 can not be directly interpreted as a false positive rate! These very high values can e.g. indicate that the generating processes are not independent.
- get_refperiod_violations(spike_trains, refperiod, progress=None)[source]¶
Return the refractory period violations in the given spike trains for the specified refractory period.
Parameters: - spike_trains (dict) – Dictionary of lists of neo.core.SpikeTrain objects.
- refperiod (Quantity scalar) – The refractory period (time).
- progress (progress_indicator.ProgressIndicator) – Set this parameter to report progress.
Returns: Two values:
- The total number of violations.
- A dictionary (with the same indices as spike_trains) of arrays with violation times (Quantity 1D with the same unit as refperiod) for each spike train.
Return type: int, dict
- overlap_fp_fn(spikes, means=None, covariances=None)[source]¶
Return dicts of tuples (False positive rate, false negative rate) indexed by unit. This function needs sklearn if covariances is not set to 'white'.
This function estimates the pairwise and total false positive and false negative rates for a number of waveform clusters. The results can be interpreted as follows: False positives are the fraction of spikes in a cluster that is estimated to belong to a different cluster (a specific cluster for pairwise results or any other cluster for total results). False negatives are the number spikes from other clusters that are estimated to belong to a given cluster (also expressed as fraction, this number can be larger than 1 in extreme cases).
Details for the calculation can be found in (Hill et al. The Journal of Neuroscience. 2011). The calculation for total false positive and false negative rates does not follow Hill et al., who propose a simple addition of pairwise probabilities. Instead, the total error probabilities are estimated using all clusters at once.
Parameters: - spikes (dict) – Dictionary, indexed by unit, of lists of spike waveforms as neo.core.Spike objects or numpy arrays. If the waveforms have multiple channels, they will be flattened automatically. All waveforms need to have the same number of samples.
- means (dict) – Dictionary, indexed by unit, of lists of spike waveforms as neo.core.Spike objects or numpy arrays. Means for units that are not in this dictionary will be estimated using the spikes. Note that if you pass 'white' for covariances and you want to provide means, they have to be whitened in the same way as the spikes. Default: None, means will be estimated from data.
- covariances (dict or str) – Dictionary, indexed by unit, of lists of covariance matrices. Covariances for units that are not in this dictionary will be estimated using the spikes. It is useful to give a covariance matrix if few spikes are present - consider using the noise covariance. If you use prewhitened spikes (i.e. all clusters are normal distributed, so their covariance matrix is the identity), you can pass 'white' here. The calculation will be much faster in this case and the sklearn package is not required. Default: None, covariances will estimated from data.
Returns: Two values:
- A dictionary (indexed by unit) of total (false positive rate, false negative rate) tuples.
- A dictionary of dictionaries, both indexed by units, of pairwise (false positive rate, false negative rate) tuples.
Return type: dict, dict
- variance_explained(spikes, means=None, noise=None)[source]¶
Returns the fraction of variance in each channel that is explained by the means.
Values below 0 or above 1 for large data sizes indicate that some assumptions were incorrect (e.g. about channel noise) and the results should not be trusted.
Parameters: - spikes (dict) – Dictionary, indexed by unit, of neo.core.SpikeTrain objects (where the waveforms member includes the spike waveforms) or lists of neo.core.Spike objects.
- means (dict) – Dictionary, indexed by unit, of lists of spike waveforms as neo.core.Spike objects or numpy arrays. Means for units that are not in this dictionary will be estimated using the spikes. Default: None - means will be estimated from given spikes.
- noise (Quantity 1D) – The known noise levels (as variance) per channel of the original data. This should be estimated from the signal periods that do not contain spikes, otherwise the explained variance could be overestimated. If None, the estimate of explained variance is done without regard for noise. Default: None
Return dict: A dictionary of arrays, both indexed by unit. If noise is None, the dictionary contains the fraction of explained variance per channel without taking noise into account. If noise is given, it contains the fraction of variance per channel explained by the means and given noise level together.
stationarity Module¶
- spike_amplitude_histogram(trains, num_bins, uniform_y_scale=True, unit=UnitQuantity('microvolt', 1e-06 * V, 'uV'), progress=None)[source]¶
Return a spike amplitude histogram.
The resulting is useful to assess the drift in spike amplitude over a longer recording. It shows histograms (one for each trains entry, e.g. segment) of maximum and minimum spike amplitudes.
Parameters: - trains (list) – A list of lists of neo.core.SpikeTrain objects. Each entry of the outer list will be one point on the x-axis (they could correspond to segments), all amplitude occurences of spikes contained in the inner list will be added up.
- num_bins (int) – Number of bins for the histograms.
- uniform_y_scale (bool) – If True, the histogram for each channel will use the same bins. Otherwise, the minimum bin range is computed separately for each channel.
- unit (Quantity) – Unit of Y-Axis.
- progress (progress_indicator.ProgressIndicator) – Set this parameter to report progress.
Returns: A tuple with three values:
- A three-dimensional histogram matrix, where the first dimension corresponds to bins, the second dimension to the entries of trains (e.g. segments) and the third dimension to channels.
- A list of the minimum amplitude value for each channel (all values will be equal if uniform_y_scale is true).
- A list of the maximum amplitude value for each channel (all values will be equal if uniform_y_scale is true).
Return type: (ndarray, list, list)
tools Module¶
- apply_to_dict(fn, dictionary, *args)[source]¶
Applies a function to all spike trains in a dictionary of spike train sequences.
Parameters: - fn (function) – Function to apply. Should take a neo.core.SpikeTrain as first argument.
- dictionary (dict) – Dictionary of sequences of neo.core.SpikeTrain objects to apply the function to.
- args – Additional arguments which will be passed to fn.
Returns: A new dictionary with the same keys as dictionary.
Return type: dict
- bin_spike_trains(trains, sampling_rate, t_start=None, t_stop=None)[source]¶
Creates binned representations of spike trains.
Parameters: - trains (dict) – A dictionary of sequences of neo.core.SpikeTrain objects.
- sampling_rate (Quantity scalar) – The sampling rate which will be used to bin the spike trains as inverse time scalar.
- t_stop (Quantity scalar) – The desired time for the end of the last bin as time scalar. It will be the maximum stop time of all spike trains if None is passed.
Returns: A dictionary (with the same indices as trains) of lists of spike train counts and the bin borders.
Return type: dict, Quantity 1D with time units
- concatenate_spike_trains(trains)[source]¶
Concatenates spike trains.
Parameters: trains (sequence) – neo.core.SpikeTrain objects to concatenate. Returns: A spike train consisting of the concatenated spike trains. The spikes will be in the order of the given spike trains and t_start and t_stop will be set to the minimum and maximum value. Return type: neo.core.SpikeTrain
- extract_spikes(train, signals, length, align_time)[source]¶
Extract spikes with waveforms from analog signals using a spike train. Spikes that are too close to the beginning or end of the shortest signal to be fully extracted are ignored.
Parameters: - train (neo.core.SpikeTrain) – The spike times.
- signals (sequence) – A sequence of neo.core.AnalogSignal objects from which the spikes are extracted. The waveforms of the returned spikes are extracted from these signals in the same order they are given.
- length (Quantity scalar) – The length of the waveform to extract as time scalar.
- align_time (Quantity scalar) – The alignment time of the spike times as time scalar. This is the time delta from the start of the extracted waveform to the exact time of the spike.
Returns: A list of neo.core.Spike objects, one for each time point in train. All returned spikes include their waveform property.
Return type: list
- maximum_spike_train_interval(trains, t_start=array(inf) * s, t_stop=array(-inf) * s)[source]¶
Computes the minimum starting time and maximum end time of all given spike trains. This yields an interval containing the spikes of all spike trains.
Parameters: - trains (dict) – A dictionary of sequences of neo.core.SpikeTrain objects.
- t_start (Quantity scalar) – Maximum starting time to return.
- t_stop (Quantity scalar) – Minimum end time to return. If None, infinity is used.
Returns: Minimum t_start time and maximum t_stop time as time scalars.
Return type: Quantity scalar, Quantity scalar
- minimum_spike_train_interval(trains, t_start=array(-inf) * s, t_stop=array(inf) * s)[source]¶
Computes the maximum starting time and minimum end time that all given spike trains share. This yields the shortest interval shared by all spike trains.
Parameters: - trains (dict) – A dictionary of sequences of neo.core.SpikeTrain objects.
- t_start (Quantity scalar) – Minimal starting time to return.
- t_stop (Quantity scalar) – Maximum end time to return. If None, infinity is used.
Returns: Maximum shared t_start time and minimum shared t_stop time as time scalars.
Return type: Quantity scalar, Quantity scalar
- remove_from_hierarchy(obj, remove_half_orphans=True)[source]¶
Removes a Neo object from the hierarchy it is embedded in. Mostly downward links are removed (except for possible links in neo.core.Spike or neo.core.SpikeTrain objects). For example, when obj is a neo.core.Segment, the link from its parent neo.core.Block will be severed. Also, all links to the segment from its spikes and spike trains will be severed.
Parameters: - obj (Neo object) – The object to be removed.
- remove_half_orphans (bool) – When True, neo.core.Spike and neo.core.SpikeTrain belonging to a neo.core.Segment or neo.core.Unit removed by this function will be removed from the hierarchy as well, even if they are still linked from a neo.core.Unit or neo.core.Segment, respectively. In this case, their links to the hierarchy defined by obj will be kept intact.