Examples¶
These examples demonstrate the usage of some functions in spykeutils. This includes the creation of a small Neo object hierarchy with toy data.
Creating the sample data¶
The functions in spykeutils work on electrophysiological data that is represented in Neo object hierarchies. Usually, you would load these objects from a file, but for the purpose of this demonstration we will manually create an object hierarchy to illustrate their structure. Note that most functions in spykeutils will also work with separate Neo data objects that are not contained in a complete hierarchy. First, we import the modules we will use:
>>> import quantities as pq
>>> import neo
>>> import scipy as sp
>>> import spykeutils.spike_train_generation as stg
We start with some container objects: two segments that represent trials and three units (representing neurons) that produced the spike trains:
>>> segments = [neo.Segment('Trial 1'), neo.Segment('Trial 2')]
>>> units = []
>>> units.append(neo.Unit('Regular intervals'))
>>> units.append(neo.Unit('Homogeneous Poisson'))
>>> units.append(neo.Unit('Modulated Poisson'))
We create some spike trains from regular intervals, a homogeneous Poisson process and a modulated Poisson process:
>>> trains = []
>>> trains.append(neo.SpikeTrain(sp.linspace(0, 10, 40) * pq.s, 10 * pq.s))
>>> trains.append(neo.SpikeTrain(sp.linspace(0, 10, 60) * pq.s, 10 * pq.s))
>>> trains.append(stg.gen_homogeneous_poisson(5 * pq.Hz, t_stop=10 * pq.s))
>>> trains.append(stg.gen_homogeneous_poisson(7 * pq.Hz, t_stop=10 * pq.s))
>>> modulation = lambda t: sp.sin(3 * sp.pi * t / 10.0 / pq.s) / 2.0 + 0.5
>>> trains.append(stg.gen_inhomogeneous_poisson(modulation, 10 * pq.Hz, t_stop=10*pq.s))
>>> trains.append(stg.gen_inhomogeneous_poisson(modulation, 10 * pq.Hz, t_stop=10*pq.s))
Next, we create analog signals using the spike trains. First, we convolve all spike times with a mock spike waveform.
>>> spike = sp.sin(-sp.linspace(0, 2 * sp.pi, 16))
>>> binned_trains = (sp.histogram(trains[0], bins=160000, range=(0,10))[0] +
... sp.histogram(trains[2], bins=160000, range=(0,10))[0] +
... sp.histogram(trains[4], bins=160000, range=(0,10))[0])
>>> train_waves = [sp.convolve(binned_trains, spike)]
>>> binned_trains = (sp.histogram(trains[1], bins=160000, range=(0,10))[0] +
... sp.histogram(trains[3], bins=160000, range=(0,10))[0] +
... sp.histogram(trains[5], bins=160000, range=(0,10))[0])
>>> train_waves.append(sp.convolve(binned_trains, spike))
Now we add Gaussian noise and create four signals in each segment:
>>> for i in range(8):
... sig = train_waves[i%2] + 0.2 * sp.randn(train_waves[i%2].shape[0])
... signal = neo.AnalogSignal(sig * pq.uV, sampling_rate=16 * pq.kHz)
... signal.segment = segments[i%2]
... segments[i%2].analogsignals.append(signal)
Now we create the relationships between the spike trains and container objects. Each unit has two spike trains, one in each segment:
>>> segments[0].spiketrains = [trains[0], trains[2], trains[4]]
>>> segments[1].spiketrains = [trains[1], trains[3], trains[5]]
>>> units[0].spiketrains = trains[:2]
>>> units[1].spiketrains = trains[2:4]
>>> units[2].spiketrains = trains[4:6]
>>> for s in segments:
... for st in s.spiketrains:
... st.segment = s
>>> for u in units:
... for st in u.spiketrains:
... st.unit = u
Now that our sample data is ready, we will use some of the function from spykeutils to analyze it.
PSTH and ISI¶
To create a peri stimulus time histogram from our spike trains, we call spykeutils.rate_estimation.psth(). This function can create multiple PSTHs and takes a dicionary of lists of spike trains. Since our spike trains were generated by three units, we will create three histograms, one for each unit:
>>> import spykeutils.rate_estimation
>>> st_dict = {}
>>> st_dict[units[0]] = units[0].spiketrains
>>> st_dict[units[1]] = units[1].spiketrains
>>> st_dict[units[2]] = units[2].spiketrains
>>> spykeutils.rate_estimation.psth(st_dict, 400 * pq.ms)[0]
{<neo.core.unit.Unit object at 0x...>: array([ 6.25, 5. , 5. , 5. , 3.75, ...
spykeutils.rate_estimation.psth() returns two values: A dictionary with the resulting histograms and a Quantity 1D with the bin edges.
If guiqwt is installed, we can also use the spykeutils.plot package to create a PSTH plot from our data (in this case we want a bar histogram and therefore only use spike trains from one unit):
>>> import spykeutils.plot
>>> spykeutils.plot.psth({units[2]: units[2].spiketrains}, bin_size=400 * pq.ms, bar_plot=True)
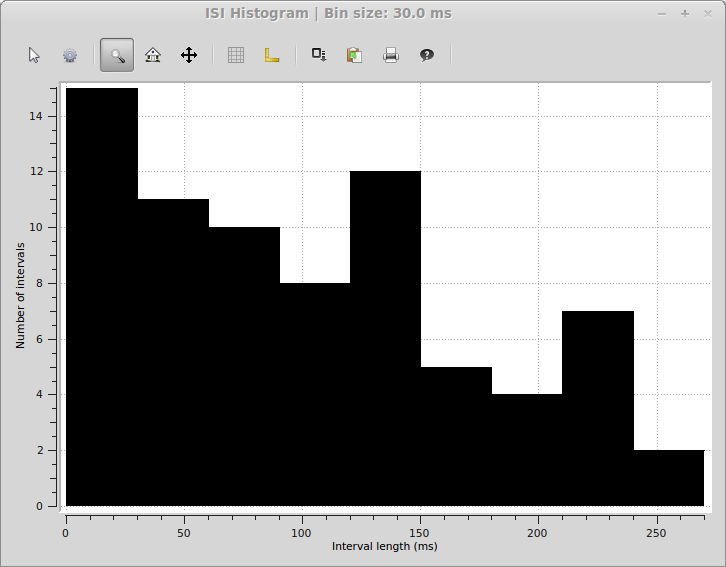
Similiarily, we can create an interspike interval histogram plot with:
>>> spykeutils.plot.isi({units[2]: units[2].spiketrains}, bin_size=30 * pq.ms, cut_off=300 * pq.ms, bar_plot=True)
This will open a plot window like the following:
Spike Density Estimation¶
Similar to a PSTH, a spike density estimation gives an esimate of the instantaneous firing rate. Instead of binning, it is based on a kernel convolution which results in a smoother estimate. Creating and SDE with spykeutils works very similar to creating a PSTH. Instead of manually choosing the size of the Gaussian kernel, spykeutils.rate_estimation.spike_density_estimation() also supports finding the optimal kernel size automatically for each unit:
>>> kernel_sizes = sp.logspace(2, 3.3, 100) * pq.ms
>>> spykeutils.rate_estimation.spike_density_estimation(st_dict, optimize_steps=kernel_sizes)[0]
{<neo.core.unit.Unit object at 0x...>: array([ ...
As with the PSTH, there is also a plot function for creating a spike density estimation. Here, we use both units because the function produces a line plot where both units can be shown at the same time:
>>> spykeutils.plot.sde(st_dict, maximum_kernel=3000*pq.ms, optimize_steps=100)
The resulting plot will look like the following:
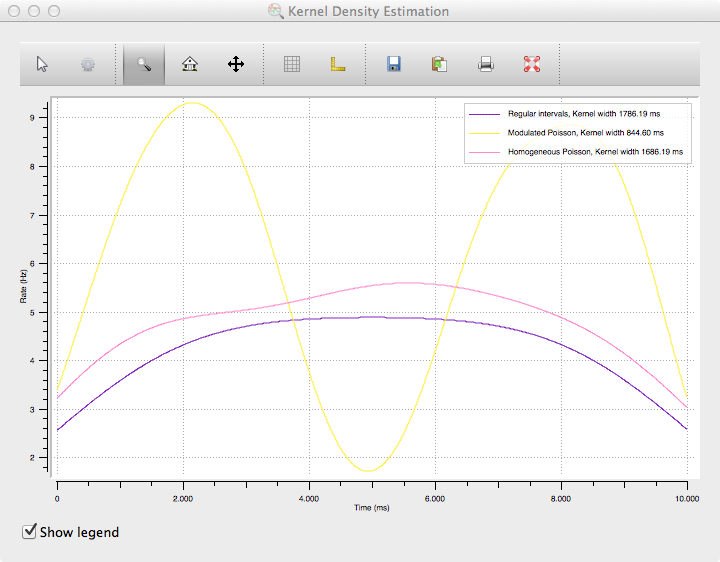
While spike density estimations are preferable to PSTHs in many cases, the picture also shows an important weakness: The estimation will generally be too low on margins. The areas where this happens become larger with kernel size, which is clearly visible from the rounded shape of the purple and pink curves (which should be flat because of the constant rate of the spike trains) with their very large kernel size.
Signal Plot¶
As a final example, we will again use the spykeutils.plot package to create a plot of the signals we created. This plot will also display the spike times from one of our spike trains.
>>> spykeutils.plot.signals(segments[0].analogsignals, spike_trains=[segments[0].spiketrains[2]], show_waveforms=False)
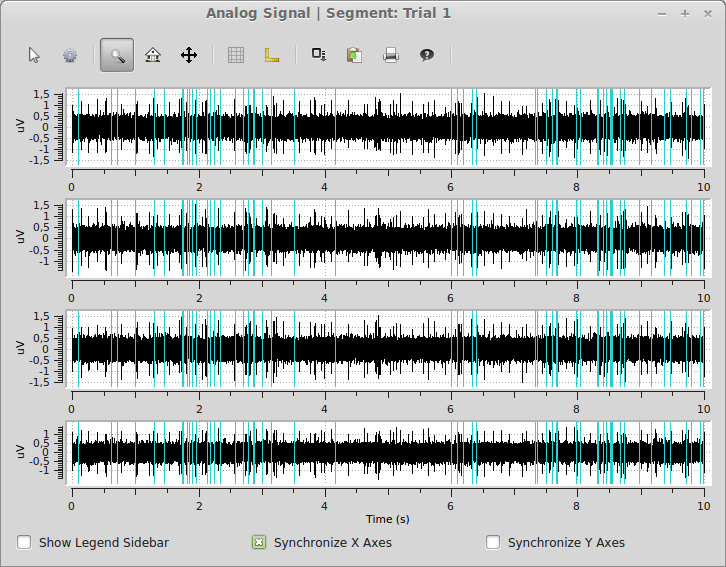
The plot shows all four signals from the first segments as well as the spike times of the inhomogeneous poisson process in the same segment.